Solution. Let the speed of the boat in still water be x km/hr
and the speed of the stream be y km/hr.
and the speed of the stream be y km/hr.
∴ Speed of the boat upstream = (x – y) km/hr
and speed of the boat downstream = (x + y) km/hr
We know that, 

According to first condition,
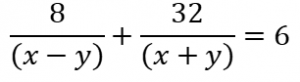 ………………. (i)
………………. (i)According to second condition,
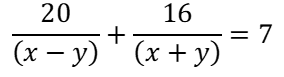 ………………. (ii)
………………. (ii)Let =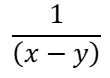 = m and
= m and 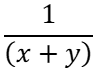 = n
= n
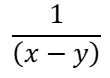 = m and
= m and 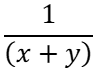 = n
= n∴ Equation No. (i) will become,
8m + 32n = 6 ………………………….(iii)
and Equation Number (ii) will become,
20m + 16n = 7 ………………………. (iv)
Multiplying equation no. (iv) by 2, we get
40m + 32n = 14 ……………………. (v)
Subtracting equation (iii) from equation (v)

∴ m =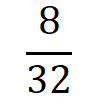
∴ m = 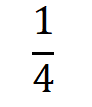
Substituting m = ¼ in equation (iii)
∴ 8m + 32n = 6
∴ 8(¼) + 32n = 6
∴ 2 + 32n = 6
∴ 32n = 6 – 2
∴ 32n = 4
∴ n = 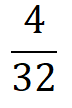
∴ n = 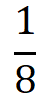
Resubstituting the values of m and n we get,
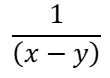 =
=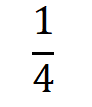
∴ x – y = 4 ……………………. (vi)
and
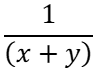 =
= ∴ x + y = 8 ……………………. (vii)
Adding equations (vi) and (vii) ,
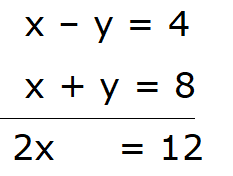
∴ x = 12/2
∴ x = 6
Substituting x = 6 in equation (vii),
∴ x + y = 8
∴ 6 + y = 8
∴ y = 8 – 6
∴ y = 2
∴ The speed of boat in still water is 6 km/hr and speed of stream is 2 km/hr