1. Study the entries in the following table and rewrite them putting the connected items in a single row.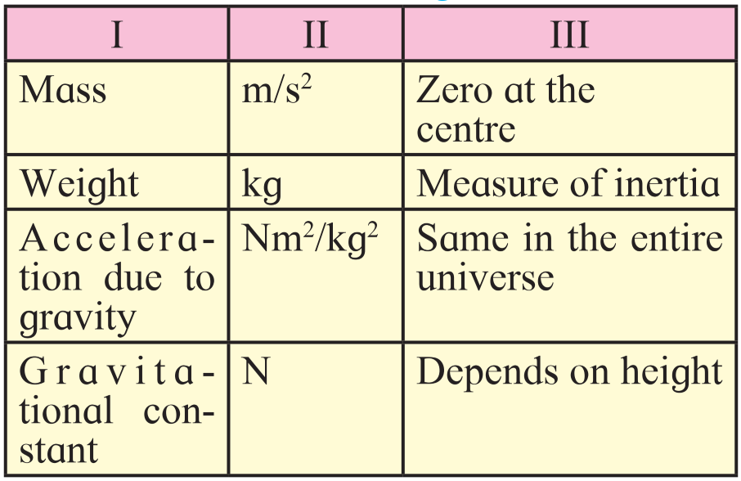
Ans.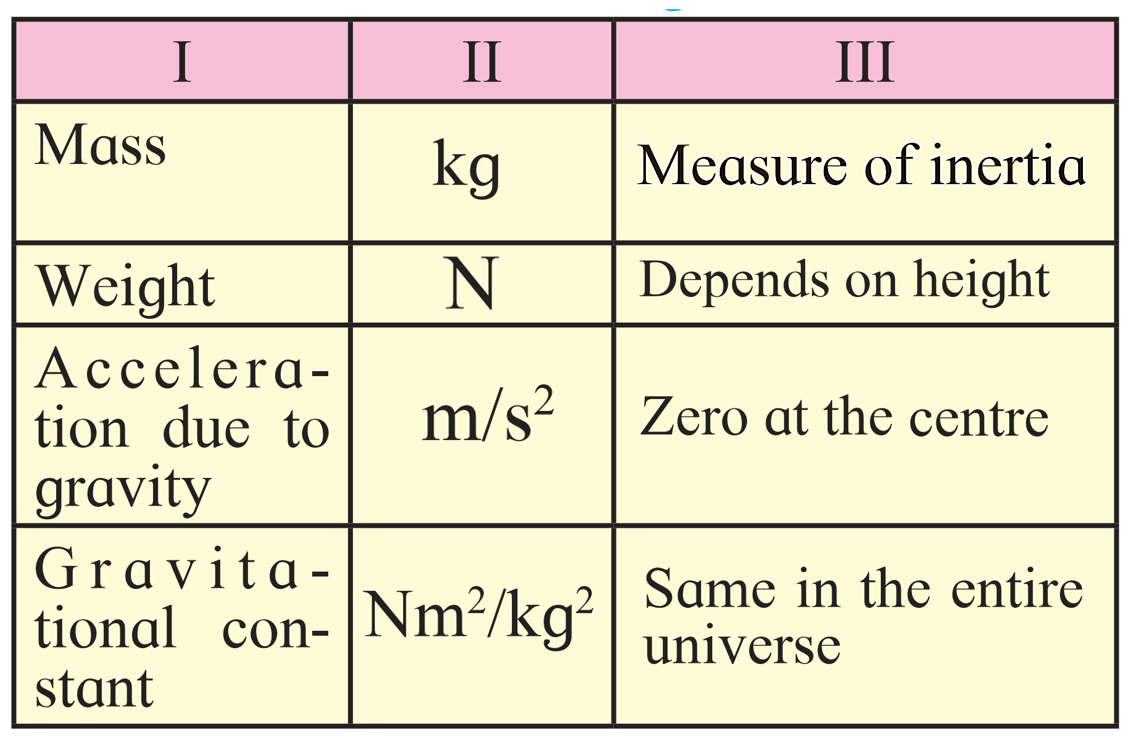
2. Answer the following questions.
a. What is the difference between mass and weight of an object. Will the mass and weight of an object on the earth be same as their values on Mars? Why?
Ans. The mass of an object is the amount of matter present in it and the weight of an object is the force with which the earth (or any other planet/ moon/star) attracts it. (1) Mass is a fundamental quantity whose value remains same everywhere. Hence, the mass of an object on earth will be same as its value on Mars. (2) Weight of an object is product of mass and gravitational acceleration,
i.e., W = F = mg
(3) As the weight depends on the value of acceleration due to gravity (g) which changes from place-to-place, and is different for earth and Mars, the weight of the object on earth will be different than its value on Mars.
b What are (i) free fall, (ii) acceleration due to gravity (iii) escape velocity (iv) centripetal force ?
Ans.
(i) Free fall: The motion of any object under the influence of the force of gravity alone is called as free fall.
(ii) Acceleration due to gravity: The acceleration produced in a body under the influence of the force of gravity alone is called acceleration due to gravity.
(iii) Escape velocity: The minimum velocity with which a body should be projected from the surface of a planet or moon, so that it escapes from the gravitational influence of the planet or moon is called as escape velocity.
(iv) Centripetal force: The force acting on any object moving in a circle and directed towards the centre of the circle is called as centripetal force.
c. Write the three laws given by Kepler. How did they help Newton to arrive at the inverse square law of gravity?
Ans.
Kepler’s three laws:
(i) Kepler’s first law : The orbit of a planet is an ellipse with the Sun at one of the foci.
(ii) Kepler’s second law : The line joining the planet and the Sun sweeps equal areas in equal intervals of time.
(iii) Kepler’s third law: The square of its period of revolution around the Sun is directly proportional to the cube of the mean distance of a planet from the Sun. ![]()
Inverse Square law of gravity
(i) If a planet revolves around the Sun in a circular orbit, then the centripetal force exerted on it by the Sun is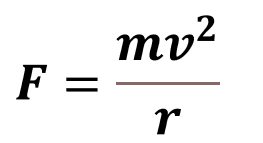
where, m-mass of the planet, v – velocity and r – radius of the circle.
(ii) Distance travelled in one revolution by the planet = Circumference = 2πr
Time period of revolution = (T)

d. A stone thrown vertically upwards with initial velocity ‘u’ reaches a height ‘h’ before coming down. Show that the time taken to go up is same as the time taken to come down.
Ans.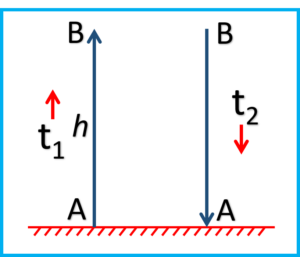
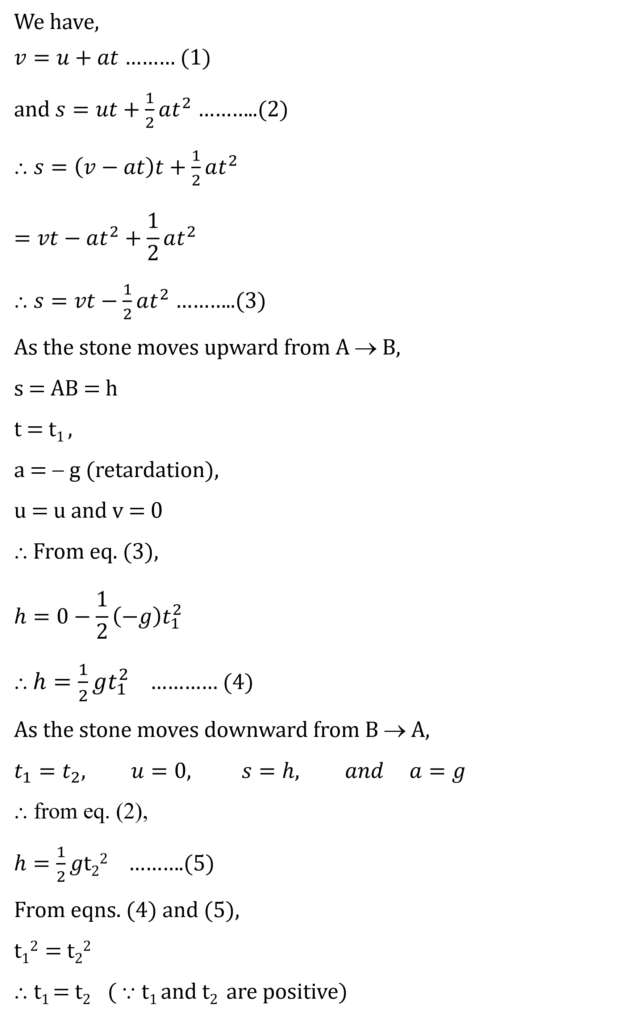
e. If the value of g suddenly becomes twice its value, it will become two times more difficult to pull a heavy object along the floor. Why?
Ans.
(i) If the value of g becomes double, the force with which the earth pulls the object i.e weight of object becomes double.
(ii) As weight increases, frictional force also increases while pulling the object
(iii) Hence, it will become two times more difficult to pull a heavy object along the floor.
3. Explain why the value of g is zero at the centre of the earth.
Ans.
As we gradually go towards the centre of the Earth, the mass of Earth under consideration goes on decreasing.
We know,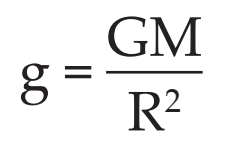
At the centre of the Earth, the mass of earth under consideration is zero, So if we substitute M = 0 in the above equation we will get the value of g as 0. Hence , g at the centre of the earth becomes zero.
4. Let the period of revolution of a planet at a distance R from a star be T. Prove that if it was at a distance of 2R from the star, its period of revolution will be √8 T.
Ans.


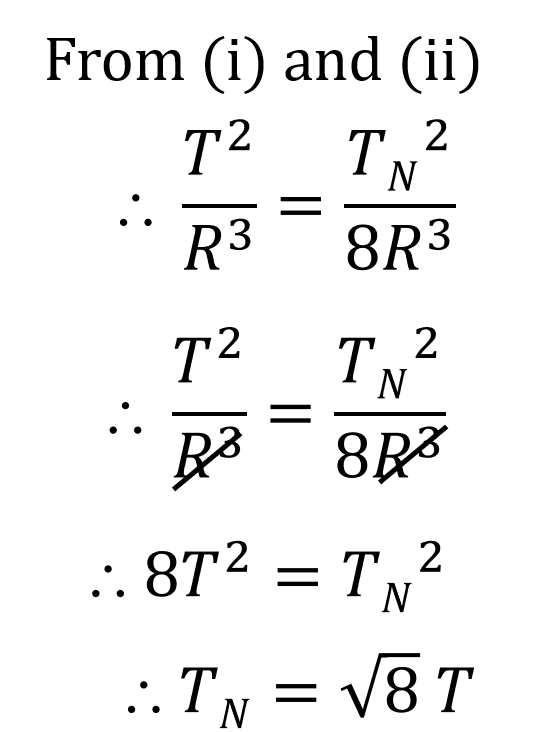
5. Solve the following examples.
a. An object takes 5 s to reach the ground from a height of 5 m on a planet. What is the value of g on the planet?
Ans.
b. The radius of planet A is half the radius of planet B. If the mass of A is MA, what must be the mass of B so that the value of g on B is half that of its value on A?
Ans.
c. The mass and weight of an object on earth are 5 kg and 49 N respectively. What will be their values on the moon? Assume that the acceleration due to gravity on the moon is 1/6th of that on the earth.
Ans.
d. An object thrown vertically upwards reaches a height of 500 m. What was its initial velocity? How long will the object take to come back to the earth? Assume g = 10 m/s2
Ans.
e. A ball falls off a table and reaches the ground in 1 s. Assuming g = 10 m/s2, calculate its speed on reaching the ground and the height of the table.
Ans.

f. The masses of the earth and moon are 6 x 1024 kg and 7.4×1022 kg, respectively. The distance between them is 3.84 x 105 km. Calculate the gravitational force of attraction between the two? Use G = 6.7 x 10-11 N m2 kg-2
Ans.
g. The mass of the earth is 6 x 1024 kg. The distance between the earth and the Sun is 1.5x 1011 m. If the gravitational force between the two is 3.5 x 1022 N, what is the mass of the Sun? Use G = 6.7 x 10-11 N m2 kg-2
Ans.
